LAQ Blog

 Through Genius Hour, I have learned quite a bit about how our eyes and corrective lenses work. Here's an overview of the key information that I've learned:

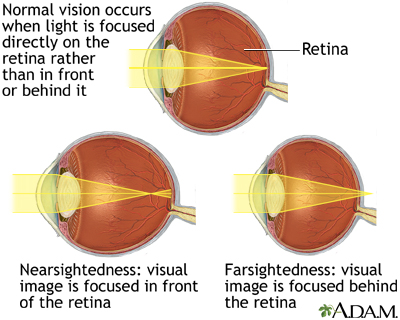
• There are three main parts of the eye that a responsible for producing an image: the front (pupil/cornea, allows light to enter), the lens (focuses light), and the retina (converts light into nerve signals). This is sort of like a camera/lens. The pupil is like the aperture blades, the lens like the focusing mechanism, and the retina like the image sensor/film plane in the body of the camera.
   
  
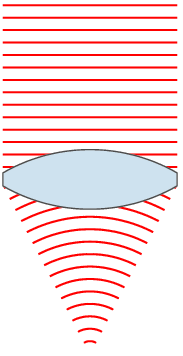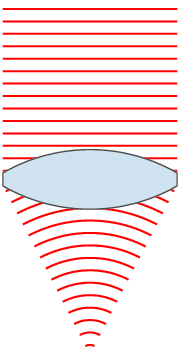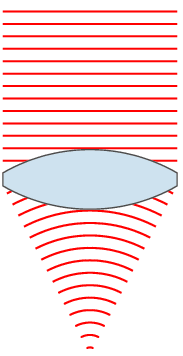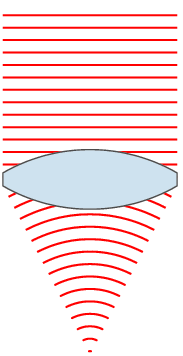
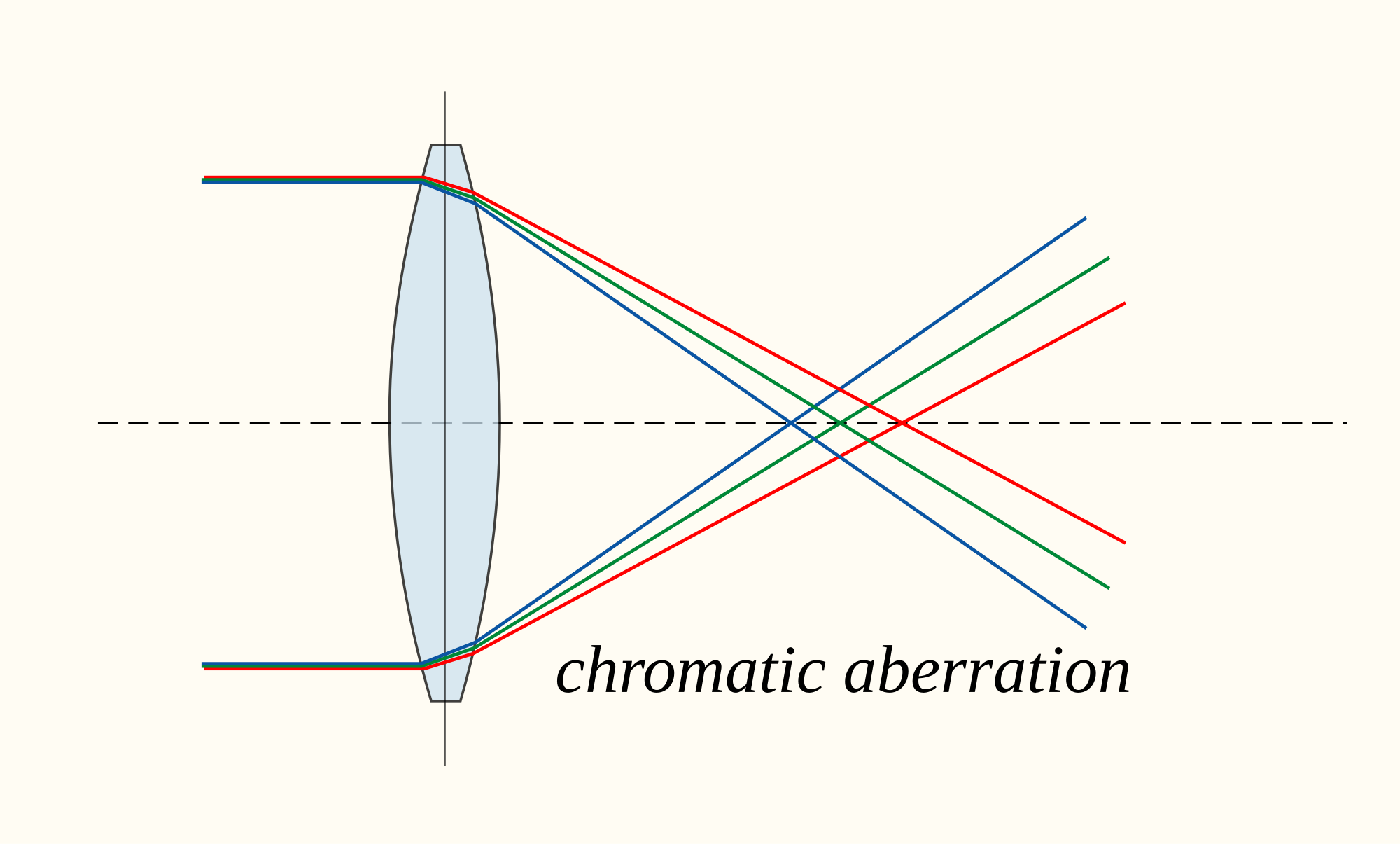
• Poor vision is often caused by irregularities in eye shape. As a result, the lens cannot change shape enough (in a process called accommodation) to focus the light onto the retina. Instead, the image is formed in front of retina (nearsightedness) or behind retina (farsightedness). 
  

• The solution to this is to refract the light before it enters the eye, so that the eye has enough power to focus the light onto retina. This is often done through corrective lenses such as eyeglasses and contacts.

For my podcast, I decided to concentrate on contact lenses because of time constraints. Here are a list of sources that I used to produce my podcast:

• https://www.cdc.gov/contactlenses/fast-facts.html (see References)
• https://www.youtube.com/watch?v=gtLDjBEFJk8
• https://www.youtube.com/watch?v=a5o289qgOAg
• https://www.fda.gov/MedicalDevices/ProductsandMedicalProcedures/HomeHealthandConsumer/ConsumerProducts/ContactLenses/ucm062319.htm
• http://www.allaboutvision.com/contacts/contact-lens-rx.htm
• https://www.ncbi.nlm.nih.gov/pubmedhealth/PMH0072432/

As I mentioned in my podcast, if we had more time, I would have loved to learn a bit more about topics such as astigmatisms, and all the prescription numbers corresponding to them. I also have some questions about different kinds of glasses, and other ways of correcting vision (i.e., laser eye surgery).

Feedback for "Genius Hour:"

Honestly, I'm a bit disappointed. I really like the concept of "Genius Hour" in that you can explore a scientific topic, but I didn't like how it was executed. It felt too constrained. 

The main factor was the mandatory blog posts. The grade should just be for the final presentation/product. The blog posts didn't help because they were just a repeat of notes, and wasted time that could have been spent on learning new information on the actual topic. The blog posts also ensured that you could not change your topic, as each blog post had to refer to the previous as an extension.

Also, the requirement of a podcast offered yet another constraint. For a topic that's literally about eyes and vision, a visual aid would have allowed for better explanations and a better understanding. I'm sure many others would have also benefited from a more free format.

I feel like a better alternative could be just allowing students to pick whatever topic they like, research it, and then deliver some sort of presentation in a time frame of maybe 1-2 weeks. This allows students to work at their own pace, and create whatever product they prefer.

Project Update I

My original idea was to research all different kinds of lenses ranging from the human eye to telescopes. However, after doing some basic research, I realized that learning about such a large spectrum would limit how in-depth my research would be. Instead, I have decided to focus (heh) on the lens of the human eye in terms of its mechanics and how it can be adjusted (i.e., eyeglasses and contact lenses).

I will strive to answer the questions that I proposed in my first post:

• How do the lenses in our eyes change shape to maintain focus?
• What do the numbers in eye prescriptions mean?

So far, I have only been able to do some research on the basic concepts behind lenses and the lenses in a human eye:

• Lenses focus rays of light because light travels more slowly in the lens than in the air, which allows the light the "bend" and focus.

animation showing the basic idea behind lenses

• The focal point or principal focus (represented by "F") is where the light beams converge.
• The focal length (represented by "f") is the distance from the center of the lens to the focal point.

graphic showing the focal point (F) and focal length (f)

• Often, multiple lenses are used in more precise equipment such as cameras and microscopes to correct for aberrations. Aberration is a term used for when a patch of light is produced instead of a single point.
• The line that runs through the centers of these lenses is known as the principal axis.

graphic demonstrating a kind of aberration

picture of chromatic aberration

•  The human eye is able to focus through tightening/relaxing of the ciliary muscle. This muscle stretches and compresses the lens within the eye, which will bend light differently depending on the shape, which allows the eye to focus.

graphic showing how the eye focuses

The two best sources I have found so far are the Encyclopedia Britannica article on optical lenses and a page on "Accommodation" of the human eye on HyperPhysics by Georgia State University.

My questions to answer for next time are:

• What do the numbers in eye prescriptions mean? 
• Why do some of us require corrective lenses (i.e., why do we need glasses/contacts?)
• How do corrective lenses work with the human eye?

Circuit Challenge #25

Circuit Challenge #25

Circuits are great fun. I even made my own.

The Setup

Total voltage: 24 V

The five resistors have resistances that are the prime numbers greater than or equal to 5.

Total Resistance

The first logical step would be to calculate the total resistance. The equations for calculating equivalent resistances are:

• in series: Req = R1 + R2 + R3 + …
• in parallel: 1/Req = 1/R1 + 1/R2 + 1/R3 + …

Because this circuit is a compound circuit, we will be using both of these equations. First, we would want to calculate the Req of the parallel circuit, which, altogether, can then be treated as “in series” with R1 and R2:

Total Current

Once we know the total resistance, we can calculate the total current because we already know the total voltage. In order to calculate the total current, we will use Ohm’s Law:

• V = I * R; (voltage = current * resistance) 
  • solved for I, it becomes: I = V/R

Individual Resistors - In Series

We can begin to calculate the voltage and current across each individual resistor now that we know the total voltage, total resistance, and total current.

We’ll start with the resistors in series: R1 and R2. In series, the current is the same everywhere (Ibattery = I1 = I2 = I3 = …). We can use the given R and I (which is equal to the total current) to calculate the voltages across each resistor with Ohm’s Law.

We can fill this information into our circuit diagram.

Individual Resistors - In Parallel

The whole parallel circuit can be treated as a single equivalent resistor that is in series with R1 and R2. In series, the total voltage is equivalent to the sum of all the individual voltages across each resistor (Vbattery = V1 + V2 + V3 + …).

Vbattery = V1 + V2 + Vparallel

24 = 7.31 + 10.234 + Vparallel

Vparallel = 6.456 V

In a parallel circuit, the voltage is the same everywhere (Vbattery = V1 = V2 = V3 = …), so we know the voltages across R3, R4, and R5 are all 6.456 V. We also know the resistances, so we can use Ohm’s Law (V = I * R or I = V/R) to calculate the current that passes through each of these resistors.

R3 R = 11 ohms V = 6.456 V I = V/R = 0.587 A

R4 R = 13 ohms V = 6.456 V I = V/R = 0.497 A

R5 R = 17 ohms V = 6.456 V I = V/R = 0.380 A

We can check that these currents are correct by adding them up to make sure they are approximately equal to the total current:

0.587 + 0.497 + 0.380 = 1.464 A ~ 1.462 A :)

All Done

We can now complete our circuit diagram:

Done. Done. Done, Heidi, SHHHHHHHHHHHHHHHHHHH. #fanggang 

Extra

Here’s a screenshot of the circuits made on an iPad:

 

We could also modify the circuit slightly. For example, we can make R3 have a resistance of 110 ohms. If we were to do this, and recalculated everything, we would observe the following:

• the Req of the parallel circuit would be larger
• the total resistance of the whole circuit would also be larger
• the total current would be smaller because resistance and current are inversely related according to Ohm’s Law (V = I * R)
• the currents across all resistors would be smaller
• if these resistors were light bulbs, they would all be dimmer
• the voltage across R1 and R2 would decrease because of the smaller current

• the voltage across the parallel circuit (R3, R4, R5) would increase in order to make the total voltage = 24 V

KWH Blog

Lenses allow humans to share our experiences through photography, explore the building blocks of life with microscopes, probe the depths of our universe with telescopes, and, most importantly, to see the world clearly.


TOPIC
The physics/concepts behind lenses such as eye lenses, camera lenses, microscope/telescope lenses, soft contact lenses, hard contact lenses, and eyeglasses.

KIND OF KNOW
My understanding is that lenses work by refracting light in a way that allows light to be focused to a certain point. For example, the lenses on cameras bend light to make it hit the sensor within the body of the camera.

WANT TO KNOW
How is light "bent?"

How do the lenses in our eyes change shape to maintain focus?
What do the numbers in eye prescriptions mean?

What do the different focal lengths of camera lenses mean?
Why are multiple elements needed within a camera lens?

Why is glass used for lenses?
What is an "index of refraction?"

HOW TO FIND ANSWERS
I will find some books/online sources about optics in physics. For subjects relating to eyes, contact lenses, or glasses, I can probably look for sources for optometry. For camera lenses and microscope lenses, I can look for information from photography-based sources.

Bumper Design

Impulse is the change in momentum, as expressed in the equation: I = Δp = pf - pi. Because of this, the unit for impulse is the same as the unit for momentum: kg-m/s. Impulse can also be defined as the product of a force and the time over which the force was applied, i.e., I = F * t.

We learned that in a collision where the impulse (or change in momentum) is the same, increasing the time over which the collision occurs will decrease the force experienced by the colliding objects. For example, a car going at a given velocity crashing into a brick wall will have the same impulse as the same car at same velocity crashing into a large air bag. However, the change in momentum will be over a longer time, which means the force experienced is less in the case of the air bag: I = Δp = F * t = F’ * t’; if F * t = F’ * t’ and t’ > t, then F’ < F.

In class, we demonstrated this principle by constructing bumpers for little carts, and measuring the forces experienced by the cart. For this experiment, we were given a plastic bag, tape, and a few sheets of paper. Because the force and time are inversely related in the case of impulse, we knew that we had to maximize the time over which the cart went from moving (non-zero momentum) to stop (zero momentum).

After some thought, we determined that the best way to achieve this was through maximizing the ability for the bumper to compress slowly. We knew that, with our given materials, the best way would have been to just crumple paper in a way that leaves a good volume of air between the folds, and then stick it in the bag. However, we decided to try a different approach which involved rolling strips of paper into little tubes. This created a “spring” effect. These springs were then wrapped in paper, which was wrapped in a plastic bag.

The idea was that the springs would provide enough resistance to not have the bumper collapse completely, but they would also be malleable enough to collapse when the cart collided. Also, because the tubes were separate from each other, we had hoped that the tubes would slide past each other, which would also increase the ability of the bumper to collapse.

TRIAL ONE

image of cart in Trial One

video of cart in Trial One

graph of Trial One

Trial One resulted in a force of approx. 1.49 N being experienced by the cart. This was pretty good, however, we knew that it could be better. We realized that our bumper did not collapse as much as we would have liked. For our redesign, we slightly unrolled the tubes to make the diameters larger, which resulted in an overall weaker spring effect. We also removed a few tubes to allow for more air/movement between the tubes.

TRIAL TWO

image of cart in Trial Two

video of cart in Trial Two

graph of Trial Two

Our redesign slightly improved our results, as the experienced force dropped to approx. 1.23 N. If we were to redesign again, we would have decreased the rigidity of the tubes even further.

Work

Work relates to energy; whenever work is done, energy is transferred. It can change the amount of kinetic or potential energy an object has. Work can be done by applying a force for a certain distance. Based on these definitions, two equations can be written:

  - W = ΔE

  - W = F * Δx

where W is work, E is energy, F is force, and x is distance. Work is measured in newton-meters (N-m), also known as joules (J).

In class, we lifted and pulled different objects to demonstrate the concepts of work in the real world. The first item we lifted was a backpack.

Using a newton meter, we were able to figure out that the applied force had to be equivalent to 46 N in order to overcome the bag’s force of gravity. We lifted the bag over a distance of 1 meter. Because we know the force applied and the distance, we can use this to calculate the work done:

  - W = F * Δx = 46 N * 1 m = 46 N-m = 46 J

This answer also represents the change in energy because W = ΔE. In this case, both the kinetic and potential energy are increasing because it goes from rest to being in motion, and its height (relative to the ground) increases.

Next, we pulled my notebook across a table over a distance of 1 meter.

For this, the force of friction had to be overcome. Once again, we used a newton meter to determine that the applied force, which turned out to be 1.7 N. We can use this to calculate the work:

  - W = F * Δx = 1.7 N * 1 m = 1.7 N-m = 1.7 J

This time, only the kinetic energy is increasing because the notebook goes from rest to motion. Potential energy does not change because the height does not change throughout the motion. This also demonstrated that if you apply work, you will become much smarter; I transformed into a THREE-AP STUDENT!

Lastly, to demonstrate a situation in which no work was done, we applied force to an object that would not move.

This made the distance in “F * Δx” equal to zero. Because, anything multiplied by zero is equal to zero, the work done is zero (despite the amazing force):

  - W = F * Δx = 4109832785917230895710298375098127 N * 0 m = 0 N-m = 0 J

Another concept that is related to work is power. Power relates to work because it is defined as the rate at which work is done (or energy is dissipated). Using this definition, we can write the equation:

  - P = W/t

where P is power, W is work, and t is time. Power is measured in watts (W), which is equivalent to 1 joule (unit of work) over 1 second (unit of time). Another unit for describing power is horsepower (hp), which is approximately 746 watts.

In class, we tried to see if we could produce power that was greater than 1 hp. This was achieved by timing someone (Mr. 3-APs) running up a flight of stairs, determining the amount of work that was required, and then calculating the power to compare with 1 hp.

Data:

  - height of stairs: 2.62 meters

  - time to climb stairs: 2.34 seconds

  - mass of person: 63 kg

The force that must be overcome is the force of gravity:

  - Fg = m * g = 63 * 9.8 = 617.4 N

Work is the applied force (equivalent to the force of gravity) multiplied by the distance:

  - W = F * Δx = 617.4 * 2.62 = 1617.588 J

Power is the rate at which work is done (W/t):

  - P = W/t = 1617.588 / 2.34 = 691.277 W

Ultimately, our runner was not able to generate more than 1 hp because 691.277 W < 746 W = 1 hp. 

Through these various activities, we were able to see the real-life applications of the work and power equations. This activity was also important because it connected to some of our previously learned concepts such as forces.

Forces Practice Problems - 11

11. A student pulls a 35 kg box up a ramp that is inclined at 12 degrees. If the box starts from rest at the bottom of the ramp and is pulled at 185 N at an angle of 25 degrees with respect to the incline, what is the acceleration of the box along the ramp? Assume the coefficient of kinetic friction is 0.27.

List of all the given values:

• mass, m = 35 kg
• angle of incline = 12°
• applied force, Fapp = 185 N, at angle = 25°
• coefficient of kinetic friction, μk = 0.27

From this, a force diagram can be drawn:

We can use trigonometry to find Fapp*x and Fapp*y:

• cos 25 = Fapp*x ÷ 185 N, Fapp*x = 185 N * cos 25 ≈ 167.667 N
• sin 25 = Fapp*y ÷ 185 N, Fapp*y = 185 N * sin 25 ≈ 78.184 N

The force of gravity Fg can be found from the equation:

• Fg = mg = 35 kg * 9.8 m/s2 = 343 N

Using this Fg value, we can also find the “x” and “y” components of Fg using trig.:

• sin 12 = Fg*x ÷ 343 N, Fg*x = 343 N * sin 12 ≈ 71.314 N
• cos 12 = Fg*y ÷ 343 N, Fg*y = 343 N * cos 12 ≈ 335.505 N

Now that we know all the “y” forces, we can calculate the FN using the Fnet*y equation:

• Fnet*y = FN + Fapp*y - Fg*y = may
• because there is no acceleration, Fnet*y = 35 kg * 0 = 0
• so, we can set FN + Fapp*y - Fg*y = 0
• fill in known values: FN + 78.184 N - 335.505 N = 0
• FN = 335.505 N - 78.184 N = 257.321 N

Using the FN and the coefficient of kinetic friction (given), we can calculate the Ff:

• Ff = μk * FN = 0.27 * 257.321 N = 69.477 N

Finally, now that we know all the “x” forces, we can calculate the Fnet*x. This can then be used to find the acceleration:

• Fnet*x = Fapp*x - Ff - Fg*x = max
• Fnet*x = 167.667 N - 69.477 N - 71.314 N = 26.876 N
• we can set this equal to max: max = 26.876
• plug in mass: 35 kg * ax = 26.876, ax ≈ 0.768 m/s2

The final answer to this problem is 0.768 m/s2.